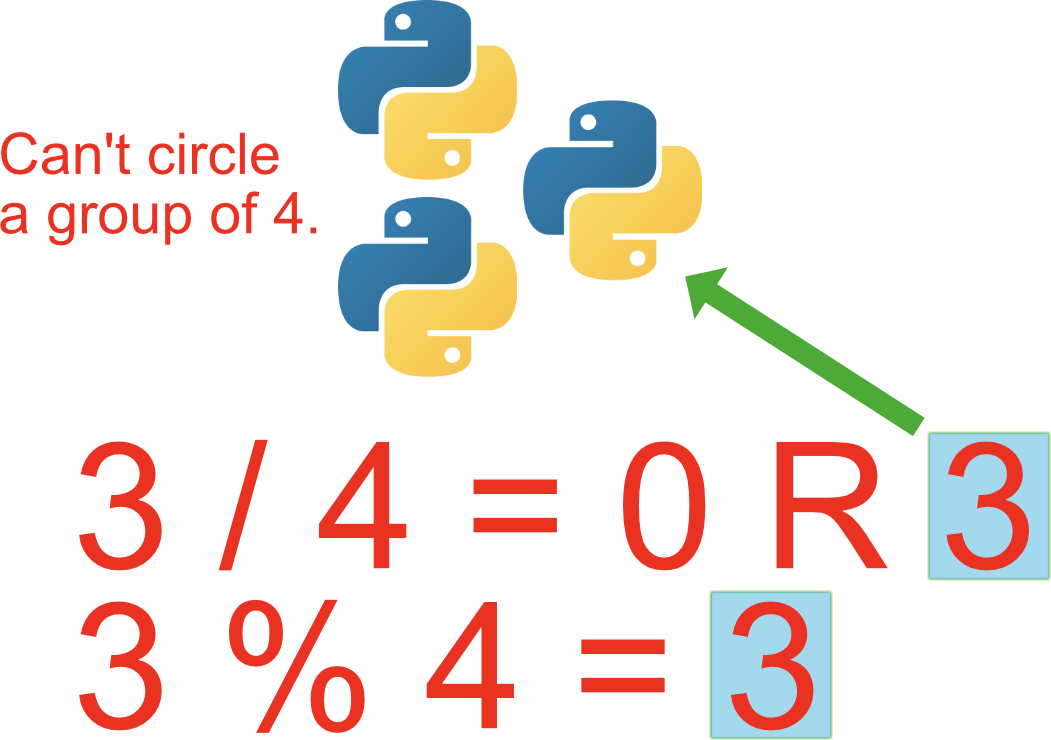This function is very useful for. Boundary properties of analytic functions and cluster sets cf.

In This Tutorial You Ll Learn About The Python Modulo Operator You Ll Look At The Mathematical Concepts Behind The Modu Modular Arithmetic Python F Names
A modular function is a function that is invariant with respect to the modular group but without the condition that f z be holomorphic in the upper half-plane among other requirements.

A modulo function. A function is called Modulus function or absolute value function if it is given by. A numeric integer value or vectormatrix resp. Given two positive numbers a and n a modulo n a n abbreviated as a mod n is the remainder of the Euclidean division of a by n where a is the dividend and n is the divisor.
It produces the magnitude of the number of variables. A that is the curvilinear triangle onto the upper half-plane where and are mapped to and respectively. The modular function gives a conformal mapping of the left half of the fundamental domain Fig.
The modulo or modulus or mod is the remainder after dividing one number by another. Remainder always integer number only. Instead of returning the result of the division the modulo operation returns the whole number remainder.
100 mod 9 equals 1 Because 1009 11 with a remainder of 1. The concept of modular arithmetic has been used by ancient Chinese and Indians for centuries. The modulo operator is used to get the remaining inches that dont evenly divide into feet.
Instead modular functions are meromorphic that is they are holomorphic on the complement of a set of isolated points which are poles of the function. 100 mod 9 equals 1 Because 100 9 11 with a remainder of 1. The mod function is useful for congruence relationships.
Modular functions have also been applied in the study of conformal mapping. R - R where y x for each x R OR fx x. 14 mod 12 equals 2 Because 1412 1 with a remainder of 2.
18 y 18 x mod 29 y 1 21 x mod 29 y 21 x 28 mod 29. Some examples may help illustrate this as its not necessarily intuitive the first time you encounter it. The modulo operator denoted by is an arithmetic operator.
A modulus function gives the magnitude of a number irrespective of its sign. In mathematics the modulus of a real number x is given by the modulus function denoted by x. The modulus function only gives a positive value of any variable or a number as the output.
For example 23 and 13 are congruent mod 5. What is the Modulus Function. As 29 is prime this is obvious.
Given two positive numbers a and n a modulo n is the remainder of the Euclidean division of a by n where a is the dividend and n is the divisor. Here we can see two function having disjoin domains on the real scale. A and b are congruent mod m if and only if modam modbm.
In MySQL the MOD function performs a modulo operation. For example 23 and 13 are congruent mod 5. Modulus Function is defined as the real valued function say f.
This function supports the following three syntaxes. Modqa b k is the modulo operator for rational numbers and returns ab mod kb and k must be coprime otherwise NA is returned. F 1 x 21 x 28.
Modn m is the modulo operator and returns n mod mmodn 0 is n and the result always has the same sign as m. If no remainder is there then it gives you 0zero as the remainder. Follow this answer to.
The major job of a modulus function is to give only non negative real outputs. 12-hour time uses modulo 12 14 oclock becomes 2 oclock It is where we end up not how many times around. It is also known as the absolute value function because it gives a non-negative value for any independent variable no matter if it is positive or negative.
You have to check that gcd 18 29 1. A modulus function is a function which gives the absolute value of a number or variable. The modulus of a given number describes the magnitude of the number.
It gives the non-negative value of x. 183 rows In computing the modulo operation returns the remainder or signed remainder of a division after one number is divided by another. The modulo operator is used to determine any remainder that may exist when the smaller unit isnt evenly divisible by the larger unit.
Mod is a mathematical function that allows us to measure the remainder in a sum. Using our friend Wolfram alpha you solve the equation. In computing the modulo operation finds the remainder or signed remainder after the division of one number by another called the modulus of the operation.
It is also called the absolute value function. The modulus operator - or more precisely the modulo operation - is a way to determine the remainder of a division operation. The modulo division operator produces the remainder of an integer division.
You provide the two values as arguments when calling the function. The Modulus Function The modulus of a number is the size of the number whether it is negative or positive for example the modulus of 6 is 6 and the modulus of -6 is 6. In this first example youll convert inches into feet.
It returns the remainder of a number divided by another number. The modulus operator finds the division with numerator by denominator which results in the remainder of the number. In other words a modulus function gives the magnitude of a number.
We use this fundamental concept whenever we tell time. 5 1. MODNM N M N MOD M The function returns the remainder of N divided by M.
The modulo or modulus or mod is the remainder after dividing one number by another. And both will leave only positive outputs which is the main role of a modulus function. Hence this is a bijection.
This function can be defined using modulus operation as follows. The modulo operation is to be distinguished from the symbol mod which refers to the modulus. The MOD function returns the rest of a division.